Đề kiểm tra chương I môn Hình học Lớp 8 (Có đáp án)

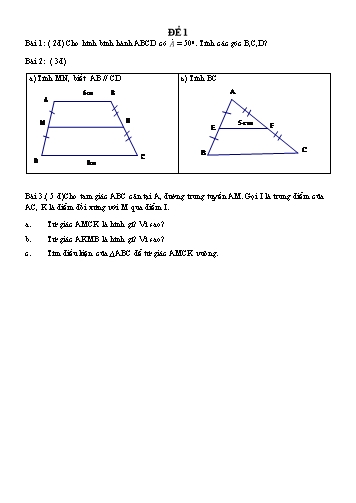
 ĐỂ 1
Bài 1: ( 2đ) Cho hình bình hành ABCD có = 500. Tính các góc B,C,D?
Bài 2: ( 3đ)
 a) Tính MN, biết AB // CD b) Tính BC
 6 cm B A
 A
 M N 5 c m
 E F
 C
 C B
 D 8cm
Bài 3.( 5 đ)Cho tam giác ABC cân tại A, đường trung tuyến AM. Gọi I là trung điểm của 
AC, K là điểm đối xứng với M qua điểm I.
a. Tứ giác AMCK là hình gì? Vì sao?
b. Tứ giác AKMB là hình gì? Vì sao?
c. Tìm điều kiện của ∆ABC để tứ giác AMCK vuông. ĐỀ 2
 Câu 1: ( 2 điểm) Tìm x, y ở hình sau:
 A 9cm B
 5cm 800
 E x F
 y 800
 D 20c C
 m
 Hình a: AB // DC
 Câu 2: ( 3 điểm) 
 Cho ABC cân tại A, D là trung điểm BC, từ D kẻ DE song song AC ( E AB ), từ D kẻ 
DF song song AB ( F AC ).Chứng minh tứ giác BEFC là hình thang cân
 Câu 3: ( 5 điểm)
Cho hình thoi ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Đường thẳng đi qua O 
không song song với AD cắt AB tại M và CD tại N.
a) Chứng minh AOM CON
b) Chứng minh tứ giác AMCN là hình bình hành
c) Cho góc AMC bằng 1380. Tính các góc còn lại của hình bình hành AMCN
 --- HẾT --- OM = ON ( AOM = CON )
OA = OC ( AOM = CON ) 0.5
Do đó, AMCN là hình bình hành (dấu hiệu 5)
c) Xét hình bình hành AMCN có:
 0.25
 0
 M = N = 138 0.25
 (tính chất hình bình 
 A = C 0.25
 Mặt khác có hành)
 + M + C + N = 3600 (tổng các góc của một tứ giác)
 + 1380 + 1380 + N = 3600 
 0 0
2 Â + 276 = 360 0.25
 0 0
2 Â = 360 - 276 0.25
2 Â = 840
 = 840 : 2
 = 420
Suy ra  = C = 420 ĐÁP ÁN ĐỀ 3
Câu Đáp án Điểm
1 Xét tứ giác ABHD có: 2
 Aˆ Dˆ Hˆ 900 (gt)
 Do đó tứ giác ABHD là hình chữ nhật
 AB = DH = 10cm
 và AD = BH
 Ta có: DC = DH + HC
 HC = DC – DH = 15 – 10 = 5cm
 Xét tam giác BHC vuông tại H, ta có: 
 BC2 = BH2 + HC2 
 BH2 = BC2 – HC2 
 = 132 - 52
 = 144
 BH = 12cm
 Mà AD = BH
 Vậy AD = 12cm hay x = 12cm.
2 Gọi góc ngoài tại đỉnh P của tứ giác là P
 1
 Ta có: P P 1800 1
 1 
 0 0 0 0
 P 180 P1 = 180 – 130 = 50
 Xét tứ giác MNPQ có:
 1
 Mˆ Nˆ Pˆ Qˆ 3600
 ˆ 0 ˆ ˆ ˆ
 M 360 N P Q 1
 = 3600 – 700 – 500 – 1300 
 = 1100
3
 0,5
 Vẽ hình và ghi GT, KL đúng
 a) Xét ABC vuông tại A, ta có: 1,5
 BC2 = AB2 + AC2
 BC2 = 62 + 82
 BC2= 100
 BC =10cm
 Vì AD là đường trung tuyến ứng với cạnh huyền BC nên
 1,5
 AD = 1 BC=5cm
 2 ĐỀ 4
Câu 1: Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O. Biết rằng: AC = 8cm, 
BD = 6cm. Tính độ dài các đoạn thẳng OA, OB, AB.
Câu 2: Cho đường thẳng d và đoạn thẳng AB như hình. Vẽ điểm A’, B’, C’ lần lượt đối xứng với 
A’, B’, C’ qua d.
Câu 3: Cho tam giác ABC cân tại A. Gọi D, E, F lần lượt là trung điểm của AB, AC. BC. Điểm I 
đối xứng F qua E
 a) Chứng minh tứ giác BDEC là hình thang cân.
 b) Chứng minh tứ giác AFCI là hình chữ nhật
 c) Tam giác cân ABC có thêm điều kiện gì thì hình chữ nhật AFCI là hình vuông. ĐỀ 5
Bài 1: ( 2 điểm )
 a) Phát biểu định lý tổng các góc của một tứ giác.
 b) Áp dụng: Cho tứ giác ABCD có Aˆ 1000 ; Bˆ 750 ;Cˆ 1350 . Tính số đo của góc D?
Bài 2: ( 3 điểm ) Cho hình thang ABCD ( AB // CD ). E; F lần lượt là trung điểm của AD 
 và BC. Gọi G là giao điểm của EF và AC. Biết rằng AB = 6cm; CD = 8cm. Tính các độ 
 dài EG và EF
Bài 3: ( 5 điểm ) Cho ∆ ABC vuông tại A. D là trung điểm của BC. Từ D kẻ DM vuông góc 
với AB tại M, DN vuông góc với AC tại N
 a) Tứ giác AMDN là hình gì? vì sao?
 b) Gọi K là điểm đối xứng với D qua N. Tứ giác ADCK là hình gì? Vì sao?
 c) Để tứ giác ADCK là hình vuông thì tam giác ABC cần có thêm điều kiện gì? ĐỀ 6
A.TRẮC NGHIỆM :(4đ) 
 Câu 1 (1đ) Các câu sau câu nào đúng, câu nào sai ?
 a) Hình thang có hai đáy bằng nhau là hình bình hành
 b) Hình bình hành có hai đường chéo vuông góc là hình thoi
 c) Hình bình hành có một góc vuông là hình chữ nhật
 d) Tứ giác có hai đường chéo bằng nhau và vuông góc với nhau là hình 
vuông 
 Câu 2 :(1đ) Nối mỗi ý ở cột 1 với mỗi ý của cột 2 thành một mệnh đề đúng :
 1- Tứ giác có 3 góc vuông là a) giao điểm của hai đường chéo
 2- Hình thoi ABCD có µA 600 b) 6 trục đối xứng
 3- Tâm đối xứng của hình bình hành là c) thì ABD là tam giác đều
 4- Hình vuông có d) hình chữ nhật
 e) 4 trục đối xứng
 Câu 3 :(1đ) 1/ Cho tứ giác ABCD, gọi M, N, P, Q lần lượt là trung điểm của các cạnh 
 AB, BC, CD, DA. Các đường chéo AC, BD có điều kiện gì thì tứ giác 
 MNPQ là hình chữ nhật?
 a) AC  BD b) AC  BD c) AC = BD
 d) AC > BD
 2/ Hình thang ABCD có AB // CD, AB= 4cm , đường trung bình EF = 
8cm.Hỏi DC = ?cm
 a) 12cm b) 16cm c) 20cm d) 32cm
 Câu 4 :(1đ) 1/ Tam giác vuông có cạnh huyền bằng 12cm. Hỏi trung tuyến ứng với 
cạnh huyền bằng :
 a) 4cm b) 12cm c) 6cm d) 
24cm
 2/ Hình thoi có hai đường chéo là 10cm và 12cm thì độ dài độ dài một 
cạnh là: a) cm b) 61 cm c) cm
 d) 11cm
 B. TỰ LUẬN : (6đ):
 Câu 5 :(2.5đ) Cho tam giác ABC vuông tại A. Điểm D thuộc cạnh BC. Gọi E và F lần 
 lượt là hình chiếu của D trên AC, AB. 
 a) Chứng minh AD = EF
 b) Xác định điểm D trên cạnh BC để tứ giác AEDF là hình vuông
 Câu 6 :(3.5đ) Cho hình bình hành ABCD. Từ A kẽ đường thẳng vuông góc với BD tại E 
 vàcắt DC tại M. Từ C kẽ đường thẳng vuông góc với BD tại F và cắt AB tại 
 N. Gọi I là trung điểm của EF.
 a) Chứng minh AE = CF
 b) Chứng minh AF = CE
 c) Chứng minh M và N đối xứng nhau qua I ĐỀ 7 
Câu 1: (3điểm) Cho hình thang ABCD( AB // CD , AB < CD). Gọi M, N lần lượt là trung điểm 
của BC và AD
 a) Chứng minh MN//AB
 b) Biết AB = 8cm, CD = 10 cm . Tính độ dài cạnh MN
Câu 2: (2điểm) Cho hình 2. Tính số đo x. Biết µA 700 , Bµ 800 , Dµ 1400 ,
 D
 C
 140° x
 70°
 A
 80°
 Hình 2
 B
Câu 3 (5 điểm) . Cho tam giác ABC vuông tại A (AB < AC). Gọi M là trung điểm BC. Qua M kẻ 
ME AB ( E AB), MF AC ( F AC ).
 a. Chứng minh tứ giác AEMF là hình chữ nhật.
 b. Tính độ dài đường chéo của hình chữ nhật AEMF biết AB = 3cm và AC = 4cm.
 c. Tìm điều kiện của tam giác ABC để tứ giác AEMF là hình vuông ·AEM 900 (ME  AB) 0.5
 ·AFM 900 (MF  AC)
Do đó tứ giác AEMF là hình chữ nhật
b) Xét ABC vuông tại A ta có:
 2 2 2
 BC AB AC (định lí Py ta go) 0.25
 0.25
 BC 2 32 42 25
 0.25
 BC 5 cm 0.25
Mà AM là đường trung tuyến ứng với cạnh BC 
 BC 5
 AM 2,5 cm 0.5
Nên 2 2 
c) Hình chữ nhật AEMF là hình vuông
 AM là đường phân giác của E· AF 0.5
 ABC cân tại A (vì khi đó AM vừa là đường trung tuyến vừa là 0.25
đường phân giác)
Vậy hình chữ nhật AEMF là hình vuông khi và chỉ khi ABC là 
tam giác vuông cân tại A 0.25