Đề kiểm tra học kì I môn Toán Lớp 9 - Trường THCS Ngô Quyền - Năm học 2017-2018 (Có đáp án)

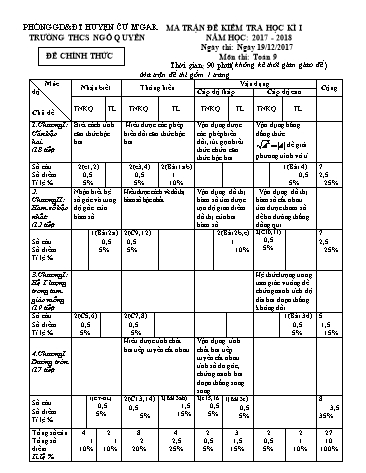
 PHÒNG GD&ĐT HUYỆN ČƯ M’GAR MA TRẬN ĐỀ KIỂM TRA HỌC KÌ I
 TRƯỜNG THCS NGÔ QUYỀN NĂM HỌC: 2017 - 2018
 Ngày thi: Ngày 19/12/2017
 ĐỀ CHÍNH THỨC Môn thi: Toán 9 
 Thời gian: 90 phút(không kể thời gian giao đề)
 Ma trận đề thi gồm 1 trang
 Mức Vận dụng
 Nhận biết Thông hiểu Cộng
 độ Cấp độ thấp Cấp độ cao
 TNKQ TL TNKQ TL TNKQ TL TNKQ TL
 Chủ đề
 1.ChươngI: Biết cách tính Hiểu được các phép Vận dụng được Vận dụng hằng 
 Căn bậc căn thức bậc biến đổi căn thức bậc các phép biến đẳng thức 
 hai hai hai đổi, rút gọnbiểu A2 A để giải 
 (18 tiết) thức chứa căn 
 thức bậc hai phương trình vô tỉ
 Số câu 2(c1,2) 2(c3,4) 2(Bài1ab) 1(Bài 4) 7
 Số điểm 0,5 0,5 1 0,5 2,5
 Tỉ lệ % 5% 5% 10% 5% 25%
 2. Nhận biết hệ Hiểu được cách vẽ đồ thị Vận dụng đồ thị . Vận dụng đồ thị 
 ChươngII: số góc và tung hàm số bậc nhất hàm số tìm được hàm số cắt nhau 
 Hàm số bậc độ gốc của tọa độ giao điểm tìm được tham số 
 nhất. hàm số. đồ thị của hai để ba đường thẳng 
 (12 tiết) hàm số đồng qui 
 1(Bài2a) 2(C9,12) 2(Bài2b,c) 2(C10,11) 7
 Số câu 0,5 0,5 1 0,5 2,5
 Số điểm 5% 5% 10% 5% 25%
 Tỉ lệ %
 3.ChươngI: Hệ thứclượng trong 
 Hệ T lượng tam giác vuông để 
 trong tam chứng minh tích độ 
 giác vuông dài hai đoạn thẳng 
 (19 tiết) không đổi.
 Số câu 2(C5,6) 2(C7,8) 1(Bài 3d) 5 
 Số điểm 0,5 0,5 0,5 1,5
 Tỉ lệ % 5% 5% 5% 15%
 Hiểu được tính chất Vận dụng tính 
 hai tiếp tuyến cắt nhau chất hai tiếp 
 4.ChươngI
 tuyến cắt nhau 
 Đường tròn 
 tính số đo góc, 
 (17 tiết)
 chứng minh hai 
 đoạn thẳng song 
 song
 1(GT-KL) 2(C13,14) 2(Bài 3ab) 2(c15,16 1(Bài 3c) 8
 Số câu
 0,5 0,5 1,5 0,5 0,5 3,5
 Số điểm
 5% 5% 15% 5% 5% 35%
 Tỉ lệ %
 Tổng sốcâu 4 2 8 4 2 3 2 2 27
 Tổng số 1 1 2 2,5 0,5 1,5 0,5 1 10
 điểm 10% 10% 20% 25% 5% 15% 5% 10% 100%
 Tỉ lệ % m m
Câu 11: Hai đường thẳng y 2 x 1 và y x 1 (m là tham số) cùng đồng biến 
 2 2
khi
A. – 2 4. C. 0 < m < 4. D. – 4 < m < - 2.
Câu 12: Cặp số ( -1; 2) là nghiệm của phương trình
A. 2x + 3y = 1 B. 2x – y = 1 C. 2x + y = 0 D. 3x – 2y = 0.
Câu 13: Cho (O; 1 cm) và dây AB = 1 cm. Khoảng cách từ tâm O đến AB bằng
 1 B. 3 cm. 3 1
A. cm. C. cm. D. cm.
 2 2 3
Câu 14: Cho đường tròn (O; 5). Dây cung MN cách tâm O một khoảng bằng 3. Khi đó:
A. MN = 8. B. MN = 4. C. MN = 3. D.kết quả khác.
 Câu 15: Nếu hai đường tròn (O); (O’) có bán kính lần lượt là 5 cm và 3 cm và khoảng 
cách hai tâm là 7 cm thì hai đường tròn
A.tiếp xúc ngoài. B.tiếp xúc trong.
C.không có điểm chung. D.cắt nhau tại hai điểm.
Câu 16: Cho (O; 6 cm), M là một điểm cách điểm O một khoảng 10 cm. Qua M kẻ tiếp 
tuyến với (O). Khi đó khoảng cách từ M đến tiếp điểm là:
A. 4 cm. B. 8 cm. C. 2 34 cm. D. 18 cm.
II. TỰ LUẬN: ( 6 điểm)
I
 1 1 x 3
Bài 1 (1 điểm): Cho biÓu thøc P . 
 x 3 x 3 x
 a/ Tìm điều kiện và rút gọn P
 b/ Tìm giá trị của x để P = 1
 4
Bài 2(1,5 điểm): Cho Hai hàm số y = 2x ( d 1 ) và y = x + 3 (d 2 )
 a)Vẽ hai đường thẳng (d 1 ) và (d 2 ) trên cùng một hệ trục tọa độ Oxy.
 b) xác định tọa độ giao điểm A của (d 1 ) và (d 2 ) bằng đồ thị và bằng phép toán.
 c) Tìm m để đường thẳng y = ( m + 4 ) x + 6 (d 3 ) và (d 1 ) , (d 2 ) đồng quy.
Bài 3 (3,0 điểm) Cho nửa đường tròn (O) đường kính AB. Gọi Ax; By là các tia vuông 
góc với AB.(Ax ; By và nửa đường tròn cùng thuộc một nửa mặt phẳng bờ AB). Qua điểm 
M thuộc nửa đường tròn ( M khác A và B), kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax tại 
C và cắt By tại D.
 a) Chứng minh CD AC BD 
 b) Chứng minh C·OD =900 
 c) AD cắt BC tại N. Chứng minh: MN / /BD
 d) Chứng minh rằng tích AC.BD không đổi khi điểm M di chuyển trên nửa đường 
 tròn.
 9x 2
Bài 4 (0,5 điểm): Cho 0< x < 2, tìm giá trị nhỏ nhất của biểu thức A 
 2 x x
 =======hết====== + Cho y = 0 x = -2 Q( -3; 0 ) trục hoành Ox 0,25 điểm
 Vẽ đường thẳng đi qua P và Q được đồ thị y = x + 3 (d 2 )
 b) Xác định được (d 1 ) cắt (d 2 ) tại A(1 ; 3) trên đồ thị và viết 
 Bài 2 được tọa độ điểm A(3;6)
(1,5điểm) * Bằng phép toán : (d 1 ) cắt (d 2 ) tại A nên phương trình hoành 0,25 điểm
 độ giao điểm là 2x = x + 3 x = 3 
 Thay x= 3 vào hàm số y = 2x y = 2. 3 = 6 
 y = 6 0,25 điểm
 Vậy tọa độ giao điểm A là :A(3;6)
 (HS vẽ dược đồ thị thì mới tính điểm câu b)
 c)Vì (d 1 ) cắt (d 2 ) tại A(1 ; 2 ) nên (d 1 ), (d 2 )và(d 3 )đồng quy
 A(3; 6) (d ) 
 3 0,25 điểm
 6 = (m + 4). 3 + 6
 3m = - 12
 m = - 4 
 0,25 điểm
 Vẽ hình Ghi GT và két luận 0,5 điểm
 y
 x
 D
 M
 C
 N
 a)Chứng minh: CD = AC+BD
 B
 Ta có: A O
 CM = CA ( CM; CA là 2 tiếp tuyến) 0,25 điểm
 DM = DB ( DM; DB là 2 tiếp tuyến)
 Cộng theo vế ta được: 0,25 điểm
Bài 3 CM + DM = CA + DB 0,25 điểm
(3,0điểm) Hay CD = CA +BD.
 b) Chứng minh C·OD = 900
 Theo tính chất của hai tiếp tuyến cắt nhau thì : 0,25 điểm
 OC là phân giác của góc AOM
 OD là phân giác của góc BOM
 0,25 điểm
 Mà Góc AOM và góc BOM là hai góc kề bù nên OC  OD hay 
 0,25 điểm
 C·OD = 900
 c) Chứng minh MN song song với BD
 Ta có AC / /BD ( cùng vuông góc với AB)
 CN CA 0,25 iểm
 mà CA CM ; BD MD (cmt)
 NB BD
 CN CM
 MN / /BD (định lí đảo Talet) 0,25 điểm
 NB MD
 d) Ta có OM  CD (tính chất của tiếp tuyến) 
 0,25điểm
 Suy ra:CM.MD = OM2 = R(hệ thức lượng trong tam giác vuông)