Đề kiểm tra tham khảo chương IV mônHình học Lớp 9 - Năm học 2019-2020 (Có đáp án)

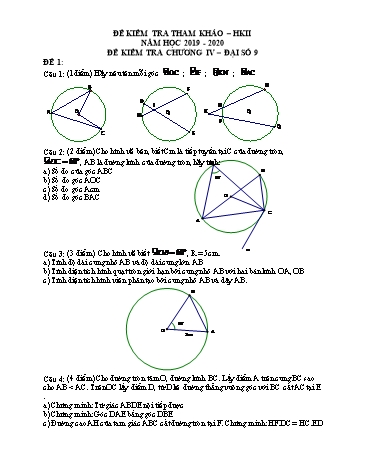
 ĐỀ KIỂM TRA THAM KHẢO – HKII
 NĂM HỌC 2019 - 2020
 ĐỀ KIỂM TRA CHƯƠNG IV – ĐẠI SỐ 9
ĐỀ 1:
Câu 1: (1điểm) Hãy nêu tên mỗi góc B· OC ; E¶IF ; Q· KN ; B· AC
 N
 B F
 D
 I M
 A O O K O
 H
 P
 Q
 C E
Câu 2: (2 điểm) Cho hình vẽ bên, biết Cm là tiếp tuyến tại C của đường tròn, 
 ·ADC 600 , AB là đường kính của đường tròn, hãy tính:D
a) Số đo của góc ABC B
b) Số đo góc AOC 60°
c) Số đo góc Acm
d) Số đo góc BAC O
 C
 A
Câu 3: (3 điểm) Cho hình vẽ biết ·AOB 600 , R = 5cm. m
a) Tính độ dài cung nhỏ AB và độ dài cung lớn AB
b) Tính diện tích hình quạt tròn giới hạn bởi cung nhỏ AB với hai bán kính OA, OB
c) Tính diện tích hình viên phân tạo bởi cung nhỏ AB và dây AB.
 B
 60°
 O
 5cm A
Câu 4: (4 điểm) Cho đường tròn tâm O, đường kính BC. Lấy điểm A trên cung BC sao 
cho AB < AC. Trên OC lấy điểm D, từ D kẻ đường thẳng vuông góc với BC cắt AC tại E 
.
a) Chứng minh: Tứ giác ABDE nội tiếp được 
b) Chứng minh: Góc DAE bằng góc DBE
c) Đường cao AH của tam giác ABC cắt đường tròn tại F. Chứng minh: HF.DC = HC.ED A
 E
 0,5
 B
 H C
 O D
 4
(4đ)
 F
 Chứng minh: Tứ giác ABDE nội tiếp được
 Xét tứ giác ABDE
 a B· AE 900 (góc nội tiếp chắn nửa đường tròn tâm O) 0,25
 0,25
 B· DE 900 ED  BC 
 B· AE B· DE 900 900 1800 0,25
 Vậy tứ giác ABDE nội tiếp 0,25
 Chứng minh: Góc DAE bằng góc DBE
 b Xét tứ giác ABDE nội tiếp:
 D· AE D· BE (hai góc nội tiếp cùng chắn cung DE) 0,5
 Chứng minh: HF.DC = HC.ED
 Xét đường tròn (O)
 OB  AF tại H B»A B»F 0,25
 Do đó: E· CD F· CH (hai góc nội tiếp chắn hai cung bằng nhau)
 0,25
 Xét HFC và DEC
 c
 F· HC E· DC 900 
 E· CD F· CH (cmt) 0,25
 HFC đồng dạng với DEC 
 HF HC
 DE DC 0,25
 HF.DC = HC.ED
 Chứng minh BC là tia phân giác của góc ABF
 Ta có B»A B»F BA = BF (liên hệ giữa cung và dây) 0,25
 d Do đó tam giác BAF là tam giác cân tại B 0,25
 Mà: BH là đường cao nên đồng thời là đường phân giác 0,25
 Vậy: BC là tia phân giác của góc ABF 0,25 2a
 0.5đ
 a) Xét tứ giác OBHA có:
 O· BH 900 ( BH là tiếp tuyến của đường tròn (O) tại B)
 0.5 đ
 O· AH 900 (AH là tiếp tuyến của đường tròn (O) tại A)
 0.5 đ
 Nên O· BH O· AH 1800
 0.5 đ
 ⇒ Tứ giác OBHA là tứ giác nội tiếp (tổng số đo hai góc đối 
 bằng 1800) 0.5 đ
2b b) Ta có: OA vuông góc dây BC tại K, 0BC cân tại O (vì 
 OB = OC) nên OK là đường trung trực của BC.
 ⇒ AB = AC ⇒ sđ »AB = sđ »AC 0.5 đ
 · ·
 ⇒ BAH = ABC (góc nội tiếp và góc tạo bởi tiếp tuyến và dây 0.5 đ
 cung chắn 2 cung bằng nhau)
 Tứ giác ABMC nội tiếp (O)
 ⇒ N· MC ·ABC (2 góc nội tiếp cùng chắn cung AC)
 0.5 đ
 Do đó: N· MC B· AH
 0.5 đ
2c c) Hai tiếp tuyến HA và HB cắt nhau tại H
 ⇒ ΔHAB cân tại H ⇒ B· AH H· BA 0.5 đ
 Theo ý b) N· MC B· AH ĐỀ 3
 Bài 1. (4 điểm ) Cho ABC có = 450 nội tiếp đường tròn (O ; 4). Gọi cung nhỏ 
 AB là cung AmB
 a) Tính chu vi và diện tích hình tròn tâm O;
 b) Tính diện tích hình quạt OAmB (ứng với cung nhỏ AB);
 c) Tính diện tích hình viên phân (ứng với cung nhỏ AB). 
 (kết quả giữ nguyên ) 
 Bài 2. (6 điểm) : Cho tam giác ABC vuông tại A ( AB > AC ) . Trên AC lấy điểm M sao 
cho AM < MC . Dựng đường tròn (O) đường kính MC , đường thẳng BM cắt (O) tại D , 
AD cắt (O) tại I .
 a) Chứng minh tứ giác ABCD nội tiếp được .
 b) Chứng minh CA là phân giác của góc ICB .
 c) Chứng minh : AC . MC = BC. IC
 d) Biết AC = 6cm , AB = 8cm và IC = 3cm . Tính MC . 
 .
 ==========Hết========
 Đáp án và thang điểm
 Bài Nội dung Điểm
 1 Vẽ hình đúng đủ 0,5
 a) 
 – Tính được C (O) = 2 .4 = 8 (cm) 0,5
 2 2
 – Tính được S (O) = .4 = 16 (cm ) 0,5
 b) 
 – Tính được sđ AmB = 900 0,5
 0,75 Ta có : BC2 = AB2 + AC2 ( định lý Py-ta-go ) 0,25
 BC2 = 100
 BC = 10 (cm)
 Mà : AC . MC = BC . IC ( chứng minh trên ) 0,25
 6 . MC = 10 . 3
 MC = 5 (cm) 0,25
. 
 ĐỀ 4 II. ĐÁP ÁN - BIỂU ĐIỂM:
 Câu Nội dung Điểm
 B· OC góc ở tâm 0.25
 E¶IF góc có đỉnh bên trong đường tròn 0.25
1 ·
 QKN góc có đỉnh bên ngoài đường tròn 0.25
 B· AC góc nội tiếp
 0.25
 D
 60
 B
 O
 A C
 m
 1 0.25
 A· BC sđ A»C (góc nội tiếp) 
 2
 1
 A· DC sđ A»C (góc nội tiếp)
 2
2
 1 0.25
 A· BC A· DC ( sđ A»C )
 a 2
 · 0
 ABC 60 0.25
 0.25
 ·AOC = sđ A»C (góc ở tâm) 0.25
 1
 b Mà A· DC sđ A»C 0.25
 2 A· FC 900 (gt) và A· EC 900 (gt) 0.5
 => A· FC = A· EC = 90o 0.25
b
 => Tứ giác AFEC nội tiếp đường tròn đường kính AC. 0.25
 Qua B vẽ tiếp tuyến Bn với (O) Bn  OB (1) ( tính chất tiếp tuyến ) 0.25
 Có: n· BA = B· CA (góc tạo bởi tia tiếp tuyến và dây và góc nội tiếp cùng chắn 
 A»B ) và B· FE = B· CA ( góc ngoài tại đỉnh F của tứ giác AFEC nội tiếp ) 0.25
c
 => n· BA = B· FE 
 => Bn // EF (2) 0.25
 Từ (1) và (2) => OB  EF 0.25 C 10 
 R = 5 (cm) 0,75đ
 2 2 
 S = R2 = .52 = 25 (cm2)
 1đ
Bài A
2(4đ)
 450
 O
 ?
 B ? C
 x
 Tính đúng góc BOC = 900 0.5đ
a)
 Tính đúng góc BCx = 450 0.5đ 
 - Tính được sđ B»C 900 0,5đ
b)
 - Tính đúng độ dài cung nhỏ BC : l = 3 (cm)
 2
 0.5đ
 9 2 2
 - Tính đươc Squạt COB = (cm ) 7,1(cm )
 4 0,75đ
c)
 9 2 2
 - Tính đươc: S COB (cm ) 4,5(cm )
 2 0.75đ
 - Tính được: Sviên phân = Squạt COB - S COB
 9 9
 = 2,6(cm2 ) 
 4 2 0,5đ
 Bài 3 - Vẽ đúng hình 0.5đ
 (4đ) ĐỀ 6
Câu 1: (4 điểm)
1)Viết công thức tính diện tích hình tròn và diện tích hình quạt tròn cung tròn n0 
2)Cho hình vẽ
 x
 C
 m
 A O B
 D
Biết Cx là tiếp tuyến tại C của đường tròn (O), C· AB = 600, AB là đường kính của đường 
tròn, AB = 6cm. Tính:
 a)Số đo góc BOC 
 b)Số đo góc BCx
 c)Số đo góc CDB
 d)Độ dài cung BmC và diện tích hình quạt tròn OBmC 
Bài 2: (6điểm) Cho đường tròn (O) đường kính BC, A là một điểm thuộc (O) sao cho AB < 
AC, D là điểm giữa O và C. Đường thẳng vuông góc với BC tại D cắt AC tại E và cắt đường 
thẳng AB tại F.
 a) Chứng minh các tứ giác ABDE và ADCF nội tiếp.
 b) Chứng minh: A· EF A· BC 
 c) Tiếp tuyến tại A của (O) cắt DE tại M. Chứng minh tam giác AME cân tại M.
 d) Gọi I là tâm đường tròn ngoại tiếp tứ giác ADCF. Chứng minh OI vuông góc với AC
 HẾT F
 M
 A
 I
 E
 B O D C
 *Chứng minh tứ giác ABDE nội tiếp đường tròn  
 0
 B· AC 90 ( góc nội tiếp chắn nửa đường tròn (O)) 1,5đ 
 B· DE 900 (gt) 0,5đ
 Tứ giác ABDE có B· AE B· DE 900 900 1800 nên nội tiếp đường 0,5đ
 tròn 0,5đ
a *Chứng minh tứ giác ADCF nội tiếp đường tròn  
 C· AF 900 (Kề bù với B· AC ) 1,5đ 
 C· DF 900 (gt) 0,5đ
 Tứ giác ADCF có 2 đỉnh A và D kề nhau cùng nhìn cạnh CF dưới một 0,5đ
 góc bằng nhau nên là tứ giác nội tiếp. 
 0,5đ
 Chứng minh: A· EF A· BC  
 A· EF A· ED 1800 ( 2 góc kề bù) 1đ
b A· BD A· ED 1800 (ABDE là tứ giác nội tiếp) 0,25đ
 Suy ra A· BC A· EF
 0,5đ
 0,25đ
 Chứng minh tam giác AME cân tại M.  
 M· AE A· BC (cùng chắn cung AC của đường tròn O) 1đ 
c A· EF A· BC (cmt) 0,5đ
 Suy ra M· AE A· EF hay AME cân tại M. 0,25đ
 0,25đ
 Tứ giác ADCF nội tiếp (cmt) mà C· DF 900 (gt) nên CF là đường kính 
d 
 của đường tròn ngoại tiếp tứ giác ADCF. Vậy tâm I của đường tròn 0,5đ