Đề thi học sinh giỏi cấp trường môn Toán Lớp 9 - Trường THCS Ngô Quyền - Năm học 2017-2018 (Có đáp án)

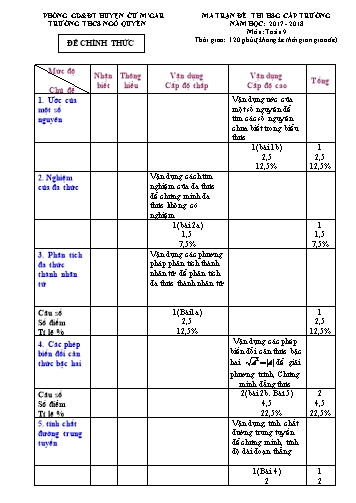
 PHÒNG GD&ĐT HUYỆN ČƯ M’GAR MA TRẬN ĐỀ THI HSG CẤP TRƯỜNG
 TRƯỜNG THCS NGÔ QUYỀN NĂM HỌC: 2017 - 2018
 Môn: Toán 9
 ĐỀ CHÍNH THỨC Thời gian: 120 phút (không kể thời gian giao đề)
 Mức độ
 Nhận Thông Vận dụng Vận dụng
 Tổng
 biết hiểu Cấp độ thấp Cấp độ cao
 Chủ đề
1. Ước của Vận dụng ước của 
một số một số nguyên để 
nguyên tìm các số nguyên 
 chưa biết trong biểu 
 thức
 1(bài 1b) 1
 2,5 2,5
 12,5% 12,5%
2. Nghiệm Vận dụng cách tìm 
của đa thức nghiệm của đa thức 
 để chứng minh đa 
 thức không có 
 nghiệm
 1(bài 2a) 1
 1,5 1,5
 7,5% 7,5%
3. Phân tích Vận dụng các phương 
đa thức pháp phân tích thành 
thành nhân nhân tử để phân tích 
tử đa thức thành nhân tử
Câu số 1(Bài1a) 1
Số điểm 2,5 2,5
Tỉ lệ % 12,5% 12,5%
4. Các phép Vận dụng các phép 
biến đổi căn biến đổi căn thức bậc 
thức bậc hai hai A2 A để giải 
 phương trình, Chứng 
 minh đẳng thức 
Câu số 2(bài 2b. Bàì 5) 2
Số điểm 4,5 4,5
Tỉ lệ % 22,5% 22,5%
5. tính chất Vận dụng, tính chất 
đường trung đường trung tuyến 
tuyến để chứng minh, tính 
 độ dài đoạn thẳng
 1(Bài 4) 1
 2 2 PHÒNG GD&ĐT HUYỆN ČƯ M’GAR KỲ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG PHÒNG GD&ĐT HUYỆN ČƯ M’GAR KỲ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG 
 TRƯỜNG THCS NGÔ QUYỀN NĂM HỌC 2017-2018 TRƯỜNG THCS NGÔ QUYỀN NĂM HỌC 2017-2018
 Khóa thi: Ngày 20/ 10/ 2017 Khóa thi: Ngày 20/ 10/ 2017
 ĐỀ CHÍNH THỨC MÔN: TOÁN 9 ĐỀ CHÍNH THỨC MÔN: SINH HỌC 9
 Thời gian: 120 phút (không kể thời gian giao đề) Thời gian: 120 phút (không kể thời gian giao đề)
Bài 1:(5 điểm ). 
 a) Phân tích đa thức sau thành nhân tử :
 x5 + x4 + 1
 x 1 3
 b) Tìm các cặp các số nguyên x và y để cho 
 8 y 8
Bài 2: (4 điểm) 
 a, Chứng minh đa thức sau không có nghiệm:
 4x2 + 4x + 5 
 b, Giải phương trình 
 x 3 4 x 1 x 8 6 x 1 5 
Câu 3: (7 điểm) Cho tam giác ABCvuông tại A, đường cao AH (H BC). 
 Biết AB = 33cm , BC = 65cm.
 a) Tính đường cao HC.
 b) Chứng minh tam giác AHB đồng dạng tam giác CHA.
 c) Gọi AE là phân giác của góc A( E BC). Tính diện tích Tam giác AEB.
Bài 4: (2 điểm)
 Cho tam giác ABC vuông tại A các đường trung tuyến AD và BE vuông góc tại G biết 
AB = 18 . Tính cạnh huyền BC
Bài 5: (2 điểm). 
 Chứng minh A = 8 2 10 2 5 8 2 10 2 5 10 2
 -----------------------------HẾT--------------------------- 
 B H E C
 a Tính được AC = 56cm 1
 Tính được HC ≈ 48,246cm 1
 b Chứng minh được tam giác AHB đồng dạng với tam giác CHA 1,5
 C Áp dụng được tính chất đường phân giác trong của tam giác tính 
 được 
 = 
 Theo tính chất của dãy tỉ số bằng nhau suy ra: 0,5
 65 65
 = = = = 
 33 56 89
 65 0,5
 EB = . 33 24,101 (cm)
 89
 Ta có: AH.BC=AB.AC AH=(AB.AC):BC 0,5
 =(33.56):65 28,431(cm)
 1
 S = EB. AH .24,101.28,431 342,608 (cm2 ) 0,5
 2
 0,5
Bài 4 Vẽ hình ,ghi GT và KL đúng 0,5
2 điểm A
 18 E
 G
 B D C
 Áp dụng hệ thức b2 = ab/ trong Δ vuôngABE ta có: AB2 = 
 2 2 0,25
 BE.BG = BE. BE = BE2 (G là trọng tâm)
 3 3
 2 0,25
 ( 18 )2 = BE2 BE2 = 27 BE = 3 3 (đv đ đ d)
 3
 BG = 2 3 ; GE = 3 0,25
 AG2 = BG.EG = 2 3 . 3 = 6 AG = 6 (đv đ đ d)
 0,25
 3 3 6
 AD = AG (đv đ đ d)
 2 2
 0,5
 Do đó BC= 2AD = 3 6 (đv đ đ d) 
Bài 5 Áp dụng công thức “căn phức tạp”
2 điểm A 8 40 8 5 8 40 8 5
 5
 8 64 40 8 5 8 64 40 8 5
 2 2 
 8 64 40 8 5 8 64 40 8 5
 2 2 5
 5